What is an interaction?

Most engineers and physical scientists working today were educated in the school of experimentation which dictates that we vary one factor at a time.  In this way, so the theory goes, we can isolate the effect of each factor without contaminating our results with the effects of other factors.  

However, a process involving many factors will usually be more complex than this.  For example, if we determine the optimum point for one factor, how can we be sure that it will remain the optimum point at all levels of the other factors?  This last point is one of the most powerful features of Design of Experiments (DoE).  If the optimum setting of a factor is dependent on the setting of another factor then we say that there is an interaction between the two factors.

The one-factor-at-a-time approach cannot give you this crucial information on interactions.

Consider a simple example where we have a chemical process in which the yield is dependent on the temperature and the concentration of catalyst.  If we ran an experiment using the one-factor-at-a-time approach then measurements would first be taken with, say, the concentration held constant and the temperature varied in appropriate steps.  This procedure would then be repeated with the temperature constant and the concentration varying.  We would then be able to construct two plots, one showing the variation of yield versus temperature and the other showing the variation with catalyst concentration.

In considering the yield versus temperature we have to ask the important question:  Will the plot of yield versus temperature always be the same, irrespective of which concentration is used?  If this is not the case, i.e. the relationship between the yield and temperature changes, then we say that we have an interaction between the two factors, temperature and concentration.

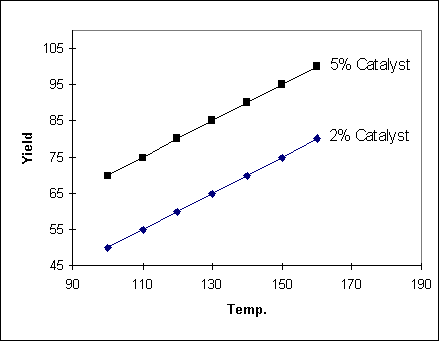
Example 1

In the following example, the change in yield with temperature does not depend on the catalyst setting (and so the two lines are parallel). Another way of saying this is that there is no interaction between Temperature and Catalyst.  In such a case the yield can be described by the equation :

Yield = aT + bC where a and b are constants and T and C are the temperature and catalyst settings respectively.

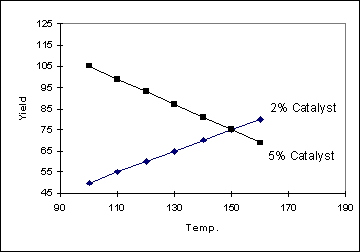
Example 2

In the following example, the change in yield with temperature does depend on the catalyst setting (and so the two lines are not parallel).  Another way of saying this is that there is an interaction between Temperature and Catalyst. The more non-parallel the lines are, the stronger the interaction is.  When an interaction is present between the factors, the yield can be described by the equation :

Yield = aT + bC + cTC where a, b and c are constants and T and C are the temperature and catalyst settings respectively.

The interaction constant, c, can be positive or negative.

The potential problems associated with the presence of interactions can be very clearly seen when we view the resulting response surface in three dimensions.